Backprop & Autograd in PyTorch Explained

This post is another in my series of things I find interesting about fastAI’s course. As most (more or less) self-taught ML folk I started with Andrew Ng’s Machine Learning Course One of the hardest assignments in that course was to implement Stochastic Gradient Descent, in Octave. While finishing that exercise was rewarding, the modern autograd mechanism is a little bit different, since we do not compute the derivatives by hand anymore. In short, below I will try to explain SGD, the whole idea of function minimization, and how it relates to Deep Learning below.

# hide
import fastbook
fastbook.setup_book()
from fastai.vision.all import *
from fastbook import *
matplotlib.rc('image', cmap='Greys')

Autograd in Pytorch

Automatic gradient computation makes modern backpropagation in machine learning possible. This autograd mechanism in Pytorch traces tensors and the operations done on them. By using this tracing, Pytorch understands how to extract the partial derivative of every parameter with respect to another (in our case, the partial derivative of the cost function with respect to the “weights” of the network). These gradients are then used to update the weights, which contributes to better “fitting” of those parameters with respect to some data points.

Let’s take a basic function to demonstrate, \(f(x)=x^2\)

def f(x):
    return x**2

Activating the autograd mechanism in PyTorch.

Thus we wish to extract the gradient, but we first need to signal to Pytorch that we wish to do this with requires_grad

xt = tensor(2.).requires_grad_()

yt = f(xt)
yt

tensor(4., grad_fn=<PowBackward0>)

As you can see, grad_fn of the pytorch tensor symbolizes that yt is dependent on some sort of Pow(er) function (as in x to the power of 2)

We calculate the gradient of xt with respect to yt at that certain point, the function tracked by PyTorch is \(y_{t} = x_{t}^{2}\) and the partial derivative is \(\frac{\partial x_{t}}{\partial y_{t}} = 2x\)

yt.backward() # compute the derivative of yt with respect to all the tensors it depends on
xt.grad # output it

tensor(4.)

Which indeed it is! \(2x_{x=2}=4\)

The Learning: SGD

And so the actual learning of a Neural Network is being done by using the same type of gradient, but at a larger scale. The gradient is used to point to the direction of steepest ascent (will increase the loss). Since we wish to minimize the loss, we subtract the gradient and go in the opposite direction, we descend. This is done many times in order to reach (hopefully) the global minima of the loss function with respect to \(W\), we call this learning \(\) W -= \alpha * gradient(W) \(\)

where \(\alpha\) is the learning rate which expresses magnitude and gradient(W) is the direction, choose a learning rate that is too small, the model will learn very slowly if at all, choose a learning rate that is too big, and you overshoot so much in the direction you will never “land” in the spot of global minima. In practice you will see the loss barely decreasing with a small \(\alpha\), and increasing widly with a big \(\alpha\).

Generating data:

We will try to fit synthetic data (we generate it instead of mining it from somewhere as seen in the first tutorial). The example here is a very simple one, but synthetic data can be used in any field with any type of data, provided you are creative enough. For example think of using a video game to generate violent footage in order to train a video classification network on the recorded video footage. Unless you are a psychopath, generating violent footage in real life is not a possibility…

Psychopath generating data for its violence detection aglorithm 🔪🔪

Since we are not adventureous, we’ll just be generating some datapoints of a quadratic-looking function, while generating some noise

time = torch.arange(0,20).float(); time
speed = torch.randn(20)*3 + 0.75*(time-9.5)**2 + 1
plt.scatter(time,speed)

<matplotlib.collections.PathCollection at 0x7feee219ca60>

And our goal is to generate a function that fits those datapoints

def f(t, params):
    a,b,c = params
    return a*(t**2) + (b*t) + c

We initialize the parameters (a,b,c) of the quadratic expression with torch.randn

params = torch.randn(3).requires_grad_()
orig_params = params.clone()

We then compute the “predictions” of \(f(t)\) at the same timesteps (same t parameter) in order to compare the predictions to the above-generated data, also known as ground truth.

preds = f(time, params)

def show_preds(preds, ax=None):
    if ax is None: ax=plt.subplots()[1]
    ax.scatter(time, speed)
    ax.scatter(time, to_np(preds), color='red')
    ax.set_ylim(-300,100)

As you can see, we did not win the RNG lottery, and the parameters (a,b,c) we randomly generated do not “fit” the datapoints, they’re actually pretty far off

show_preds(preds)

But how bad are these randomly generated parameters? Enter the loss function, which in our case is the mean squared distance between “predicted” and “generated” datapoints

def mse(preds, targets):
    return ((preds-targets)**2).mean().sqrt()
loss = mse(preds, speed)
loss

tensor(160.6979, grad_fn=<SqrtBackward>)

Now let’s do some the spicy backprop magic with backward What does backward do? Basically when we call backward on a tensor, PyTorch intelligently computes the partial derivative of that tensor with respect to every tensor that it depends on (which tensors were used in computing this end tensor).

And so in this context params.grad basically means “the partial derivative of loss with respect to params” or more formally: \(\frac{\partial loss}{\partial params}\)

loss.backward()
params.grad

tensor([-165.5151,  -10.6402,   -0.7900])

As we know, the gradient points to the location of steepest ascent, if we subtract it, we descend. We do this in order to find the minima of the loss function with respect to our quadratic function params.

Basically we are doing backprop! Still confused? Watch this example on a simple Dense Network

lr = 1e-3
params.data -= lr * params.grad.data
params.grad = None

preds = f(time, params)
mse(preds,speed)
show_preds(preds)

We can formalize all these steps in the below-defined function then!

• we extract the “predictions” of our approximated quadratic
• we measure how far off we are (loss)
• we compute the gradient of this loss with respect to our approximation
• we update the approximation (this is the learning itself folks!) And this is called an epoch

We repeat these steps until it’s not worth it anymore, in practice we stop once we either overfit (this learning does not translate well to data the model has not seen before) or we underfit (the model cannot fit the data better)

def apply_step(params, prn=True):
    preds = f(time, params)
    loss = mse(preds, speed)
    loss.backward()
    params.data -= lr * params.grad.data
    params.grad = None
    if prn: print(loss.item())
    return preds

And after many iterations we end up seeing this!

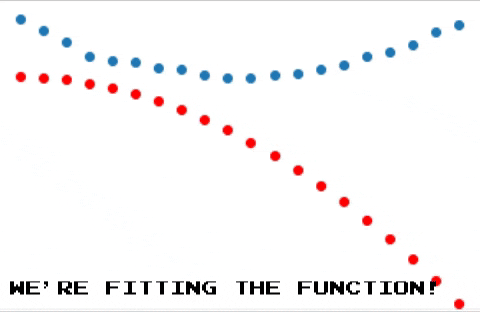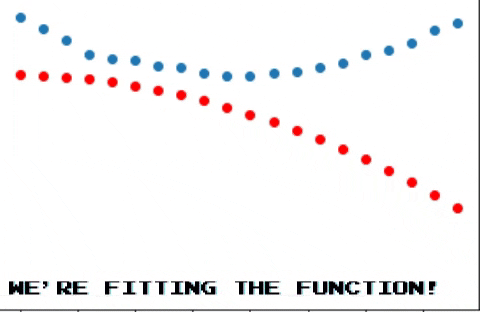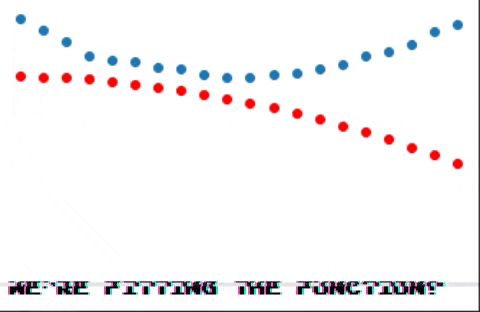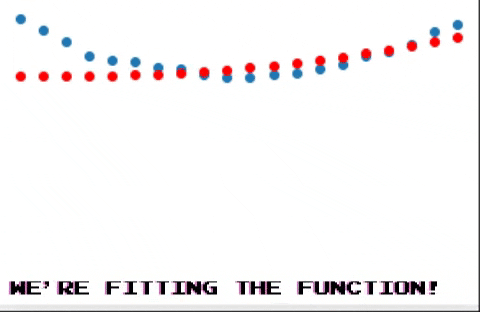
Conclusion

As you can see backpropagation is a pretty simple idea, autograd makes intuitive sense, although it seems like it kind of works by magic. In future posts I may explain what actually happens under the hood, so stay tuned! :D

Acknowledgements

This example is ripped off straight from fastAi’s course, with my own spin-off explanation, more to come!